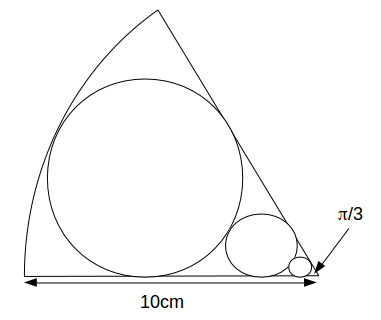
\[r+\frac{r}{sin \pi /6}=3r=10 \rightarrow r= \frac{10}{3} cm\]
.The smaller circles extend out to
\[10-2r=10- 2 \frac{10}{3}=\frac{10}{3} cm \]
from the centre.
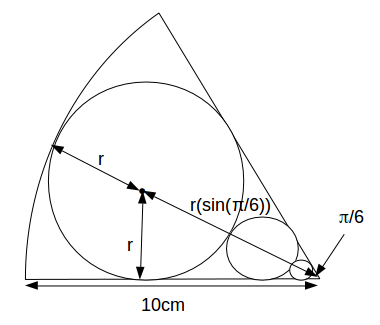
\[\frac{1}{3} \frac{10}{3} = \frac{10}{9}\]
.In general the radius of the kth largest circle will be
\[\frac{10}{3^k}\]
and the area of the circle is \[\pi (\frac{10}{3^k})^2 = \frac{100 \pi }{9^k}\]
.The areas of the circles form a geometric sequence with first term
\[a = \frac{100 \pi }{9}\]
and common ratio \[r = \frac{1}{9}\]
.The area of all the circles is
\[A= \frac{a}{1-r}=\frac{\frac{100 \pi }{9}}{1-1/9}=\frac{800 \pi}{9}\]
. 