\[L\]
is free to move subject to the ends of the line being on the positive \[x\]
and \[y\]
axes.A line drawn from the origin meets the line at a point M, such that the two lines are at right angles.
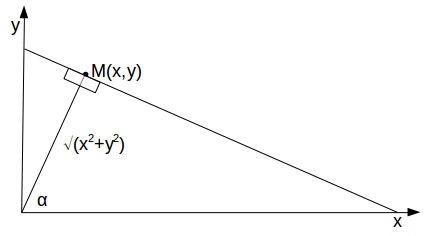
\[\alpha\]
as above, \[x=\sqrt{x^2+y^2}cos \alpha , \: y= \sqrt{x^2 +y^2} sin \alpha\]
.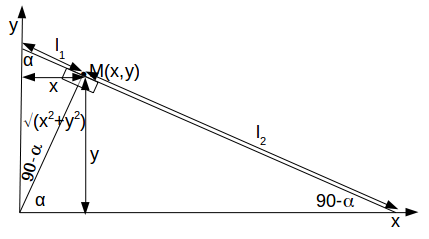
\[\begin{equation} \begin{aligned} L=L_1+L_2 &= \frac{x}{sin \alpha}+ \frac{y}{sin (90- \alpha )} \\ &= \frac{x}{sin \alpha}+ \frac{y}{cos \alpha} \\ &=\frac{x \sqrt{x^2+y^2}}{y}+ \frac{y \sqrt{x^2+y^2}}{y} \\ &= \frac{x^2 \sqrt{x^2+y^2}}{xy}+\frac{Y^2 \sqrt{x^2+y^2}}{xy} \\ &= \frac{ (\sqrt{x^2+y^2})^3}{xy} \end{aligned} \end{equation}\]
Then
\[L^2x^2y^2=(x^2+y^2)^3\]
.
