Locus of Midpoint of a Rod With Ends on the Axes

Let M be the midpoint of a line of length

\[L\]

free to move in the

\[xy\]

plane, with the ends of the line remaining on the axes. What will be the equation of the curve traced out by M?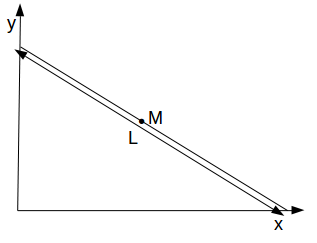

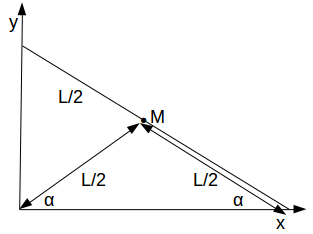
equation traced out by midpoint of line free to move with ends on axes

The triangles formed by the ends of the rod, the midpoint and the origin are isosceles.

equation traced out by midpoint of line free to move with ends on axes

The coordinates of the midpoint are

\[)L/2 cos \alpha , L/2 sin \alpha )\]

. Now use the identity

\[cos^2 \theta + sin^2 \theta =1\]

to give

\[x^2+y^2 =L^2/4\]

.

\[M\]

will trace out the quarter of a circle in the first quadrant, radius

\[L/2\]

whose sides touch the axes.