\[h\]
and depth \[d\]
is being tilted. As it tilts its apparent height increases. What angle of tilt will result in the greatest apparent height?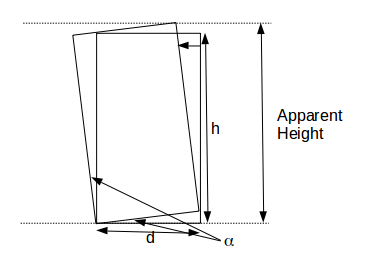
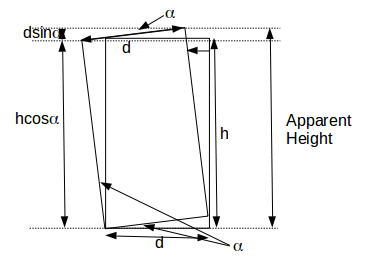
\[hcos \alpha + dsin \alpha\]
.Let
\[f(\alpha )=hcos \alpha + dsin \alpha\]
.Then
\[\frac{df}{d \alpha}=-hsin \alpha + dcos \alpha =0 \rightarrow tan \alpha = \frac{d}{h}\]
.\[\frac{d^2f}{d \alpha^2}=-hcos \alpha - dsin \alpha \lt 0\]
since \[\alpha\]
is acute. The height is a maximum and\[\begin{equation} \begin{aligned} f(\alpha)_{MAX}=d sin \alpha_{MAX}+hcos \alpha_{MAX} &= d/(cosec \alpha_{MAX})+h/(sec \alpha_{MAX}) \\ &= d/ \sqrt{1+cot^2 \alpha_{MAX}}+h/ \sqrt{1+tan \alpha_{MAX}} \\ &=d / \sqrt{1+h^2/d^2}_h/ \sqrt{1+d^2/h^2} \\ &= d^2/ \sqrt{d^2+h^2}+h^2/ \sqrt{d^2+h^2} \\ &= \sqrt{h^2+d^2} \end{aligned} \end{equation}\]
