The Local Maximum Principle

A function f defined on a region R has a local maximum at a point %alpha in R if there is some r >0 such thatandfor

For example,then f has a local maximum atOn the other handhas no local maximum at all.

Suppose thatis a non – constant analytic function with domain a regionand thatIfhas a local maximum atthen there is somesuch that

for(1)

But ifthenis an open set containingby the Open Mapping Theorem. and socontains an open disc,say, centred at

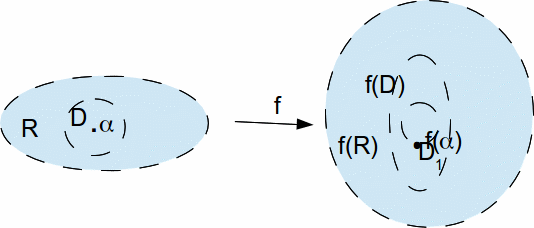
We can show that there is some pointsuch that

Ifthen this is evident becauseis non – constant.  Ifthen acan be found by extending the line segment from 0 to

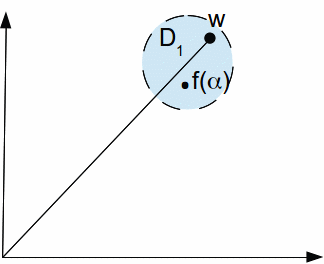
Sincewe havefor someand hence contradicting (1). The following result is proved.

The Local Maximum Principle

Let a functionbe analytic on a regionIfis non – constant onthen the functionhas a local maximum on