Using Residues to Sum a Series

Theorem

Letbe an even function analytic onexcept for poles at the pointsnone of which is an integer, and possibly at 0, and letbe the square contour with vertices atSuppose also that the functionis such that

Then

With this theorem we can find the sum of a wide range of series exactly.

Example: Prove

The functionis even and analytic onapart from a pole of order 2 at

The functionhas a pole of order 3 atThe residue atis given by

As

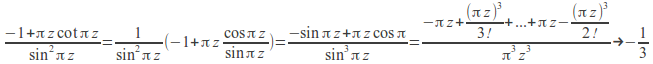
Hence

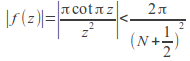Iflies on the contourthensofor

Hence by the Estimation Theorem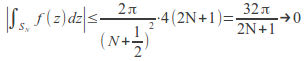as

It follows