Suppose we are required to find the exact value of
where
is an even function. We can replace the
actor by
which has simple poles at the points
with residue
This is important for summing an alternating series. Consider the function
whereis an even function analytic on
apart from a finite number of poles, none of which occur at an integer apart from 0 possible. The residue of
at a non – zero integer
is
We integrate the function
around the square contour
with corners at
where
is large enough to contain all non zero poles
of
It follows from the Residue Theorem that
sinceis even.
Now let n tend to infinity. If %phi is such that
tends to 0 astends to infinity then
so
Example: Find
The function
is even and analytic onapart from simple poles at
and similarly for the pole at
Sinceis analytic at
If
lies onthen
so
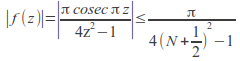for
so by the Estimation Theorem,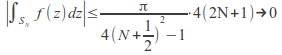
as
Hence