The Inverse Function Rule

Letbe a one to one analytic function whose domain is a regionThenis analytic onandfor

Proof: We must show thatforandis continuous on

To prove the first part note that iffor somethen by the local mapping theoremis many to one nearcontradicting thatis one to one on

To prove the second part letand putWe must show that for each there is asuch that

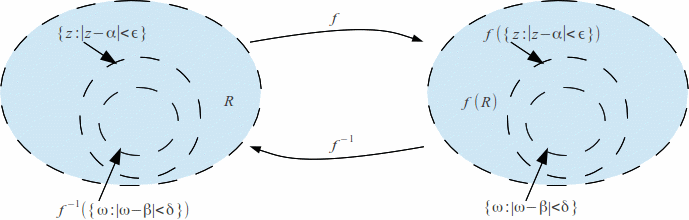
We know thatis an open set by the Open Mapping Theorem so there existssuch that

This implies that