We can define the interior, boundary and exterior of a set in using open sets.
Definition
Let
be a subset of
and let
Then
a)
is an interior point ofif there is an open disc centred atwhich lies entirely in
b)is an exterior point ofif there is an open disc in centred atwhich lies entirely outside
These definitions are illustrated below.
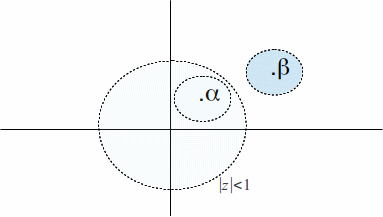
is an interior point of the set
and
is an exterior point.
The set of interior points of a setis called
and the set of exterior points is called
Ifis neither an interior or exterior point, then each open set centred atcontains at least one point ofand at least one point of
The set of such points is called the boundary of and labelled
It follows that
and
are disjoint and that
The boundary of the set of all z satisfying
is the circle
Notice that ifis the set
the interior ofis still the set of all
satisfying
so the boundary is still
Sinceand
are unions of open sets, they are also open, and
is closed.