In logic, an axiom is a postulate considered to be self evidenty that requires no proof and serves as a starting point for deducing and inferring other truths.
In maths the term is used in two related but distinguishable senses: "logical axioms" and "non-logical axioms". In both senses, an axiom is any mathematical statement that serves as a starting point from which other statements are logically derived. Unlike theorems, axioms (unless redundant) cannot be derived by principles of deduction, nor are they provable since they do not follow from any other axiom or theorem derived from an axiom.
Logical axioms are usually statements that are taken to be universally true (e.g., A and B implies A), while non-logical axioms (e.g.,
) are defining properties of a group of mathematical objects. In general, a non-logical axiom is not a self-evident truth, but rather a property used build a mathematical theory. To axiomatize a system of knowledge is to show that its claims can be derived from a complete, self consistent set of sentences (the axioms).
There are typically multiple ways to axiomatize a given system. In arithmetic, one set of axioms are the Peano axioms. These are the most widely used axiomatization of first-order arithmetic. They are a set of axioms strong enough to prove many important facts about number theory and logic and they allowed Gödel to establish his famous second incompleteness theorem.
We have a language1
where 0 is a constant symbol,
is a unary function and the following axioms:
-
-
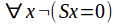
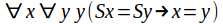
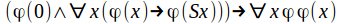or any
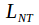formula
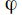with one free variable.
The standard structure is
where
is the set of natural numbers, is the successor function
and 0 is naturally interpreted as the number 0.