Pyramidal Numbers

Triangular numbers are constructed starting with a single dot, then a triangle with a dot at each vertex, then a larger triangle with a dot between each two dots and so one. If these triangles are assembled into a pyramid, then the numbers of dots are called pyramidal numbers.

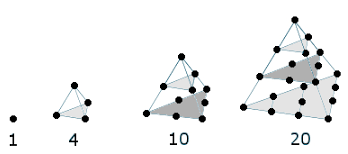
Base	Number of Dots
Triangle	\[\frac{1}{6}n(n+1)(n+2)\]
Square	\[\frac{1}{6}n(n+1)(2n+1)\]
Pentagon	\[\frac{1}{2}n^2(n+1)\]
Hexagon	\[\frac{1}{6}n(n+1)(4n-1)\]
Heptagon	\[\frac{1}{6}n(n+1)(5n-2)\]
Octagon	\[\frac{1}{2}n(n+1)(2n-1)\]
n - gon	\[\frac{1}{6}n(n+1)(n(r-2)-(r-5))\]