The
- distribution arises as the ratio of two chi-squared distributions:
where
-
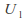and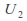
have chi-square distributions with
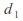and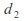
degrees of freedom respectively, and
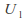- and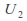are independent.
-
-
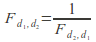
The mean, variance and skew are
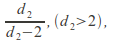
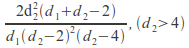and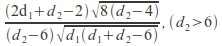 
respectively.
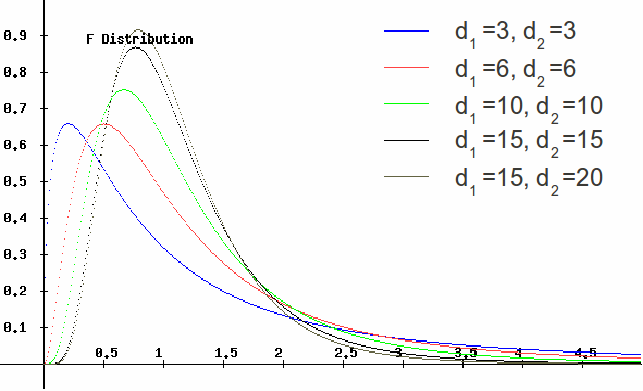
The probability density function of an
distributed random variable is given by
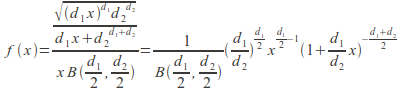for real
whereand are positive integers, and
is the beta function.
The cumulative distribution function is
where
is the regularized incomplete beta function.