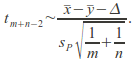Two Sample t - Test
The two sample t – test is one of the most useful and widely used statistical tests. It tests for the equality of the means of two samples, subject to the assumptions:
The two sample both arise from normal distributions.
The variances of the populations of the two samples are the same. In practice we do not usually know the population variance and must use the sample variance as an estimator. If the two sample variances are not 'too dissimilar', then the population variances are often assumed to be the same.
The t test is so useful because the data does not need to be paired in any way, and takes all the data into account to give the most reliable results.
First define the pooled standard deviation
If the sample sizes are
and m respectively and the standard deviations are
and
respectively then
The null distribution for two samples from populations
and
with
sample means
and
assuming the conditions above are met is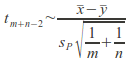
where
is the pooled standard deviation.
Example: The data below is for compression strength of cans of cola and strawberryade.
Drink | Sample Size | Sample Mean | Standard Deviation |
Strawberryade | 15 | 540 | 21 |
Cola | 14 | 554 | 15 |
Does the higher carbonation of cola suggest higher compressive strength?
The null and alternative hypotheses are
and
respectively. The test is one sided.
The test statistic is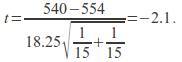
At significance level of
We do not reject the null hypothesis at this level.
We can also test the two sample for a mean difference of
with
using
