\[\int_S \mathbf{F} \cdot \mathbf{S} = \int_S \mathbf{F} \cdot \mathbf{n} dS\]
For a plane surface
\[\mathbf{n}\]
is a constant vector and this can make the calculation quite simple.
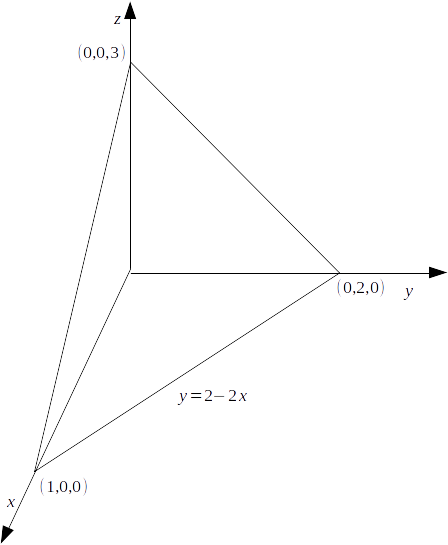
Consider the flux of the vector field \[\mathbf{F} = xy \mathbf{i} + y^2 \mathbf{j} + yz \mathbf{k}\]
out of the triangular plane surface with vertices \[A(1,0,0),B(0,2,0),C(0,0,3)\]
.
\[\mathbf{n}\]
to the plane as\[\begin{equation} \begin{aligned} \mathbf{n} &= \frac{(\mathbf{OB} - \mathbf{OA}) \times (\mathbf{OC} - \mathbf{OA})}{|(\mathbf{OB} - \mathbf{OA}) \times (\mathbf{OC} - \mathbf{OA})|} \\ &= \frac{\left\{ \begin{pmatrix}-1\\2\\0\end{pmatrix} , \begin{pmatrix}-1\\0\\3\end{pmatrix} \right\}}{\left| \left\{ \begin{pmatrix}-1\\2\\0\end{pmatrix} , \begin{pmatrix}-1\\0\\3\end{pmatrix} \right\} \right|} = \frac{\begin{pmatrix}6\\3\\2\end{pmatrix}}{\sqrt{49}} = \frac{1}{7} \begin{pmatrix}6\\3\\2\end{pmatrix} \end{aligned} \end{equation}\]
Thhe equation of the plane is
\[6x+2y+3z=d\]
. To find \[d\]
substitute a point in the plane, say \[A(1,0,0)\]
, obtaining \[d=6\]
hence \[z= \frac{1}{3} (6- 6x-2y)\]
then\[\begin{equation} \begin{aligned}\int_S \mathbf{F} \cdot \mathbf{n} dS &= \frac{1}{7} \int_S 6xy + 3y^2 + 2yz dS \\ &=\frac{1}{7} \int_S 6xy+3y^2 +y(6-6x-3y) dS \\ & = \frac{1}{7} \int_S 6y dS \\ &= \frac{1}{7} \int^1_0 \int^{2-2x}_0 \frac{6y}{| \mathbf{n} \cdot \mathbf{k}|}dy dx \\ &= \frac{3/7}{2/7} \int^1_ 0 4-8x+4x^2 dx \\ &= \frac{3}{2} [4x-4x^2+\frac{4}{3}x^3]^1_0 \\ &= 2 \end{aligned} \end{equation}\]
