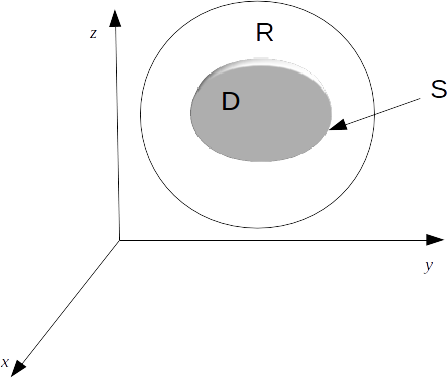
Let
\[\phi (x,y,z), \: \psi (x,y,z) \]
be harmonic functions with continuous first and second partial derivatives on a region \[R\]
containing a region \[D\]
with surface \[S\]
.
\[\int \int_S \phi (\frac{\partial \psi}{\partial n} - \frac{\partial \psi}{\partial n} ) dS =0 \]
Proof
Green's Second Theorem can be written
\[\int \int \int_V (\phi \nabla^2 \psi - \psi \nabla^2 \phi )dV = \int \int_S ( \phi \frac{\partial \psi}{\partial n} - \psi \frac{\partial \phi}{\partial n} ) dS \]
Since
\[\phi , \: \psi\]
are both harmonic on \[R\]
, \[\nabla^2 \phi = \nabla^2 \psi =0\]
Hence
\[\int \int_S \phi (\frac{\partial \psi}{\partial n} - \frac{\partial \psi}{\partial n} ) dS =0 \]
