\[\mathbf{F}\]
in spherical polar coordinates is \[\mathbf{F} = F_r \mathbf{e_r} + F_\theta \mathbf{e+\theta} + F_\phi \mathbf{e_\phi}\]
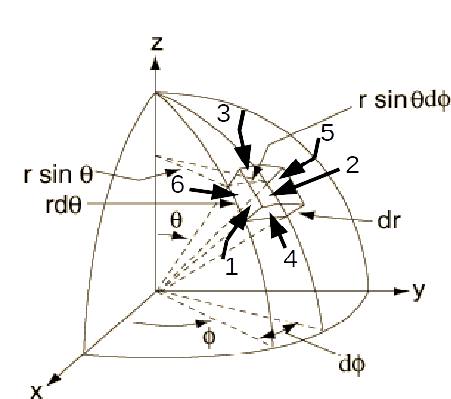
\[\begin{equation} \begin{aligned} \int_S \mathbf{F} \cdot d \mathbf{S} &= (F)r sin \theta r d \theta d \phi)_2 - (F)r sin \theta r d \theta d \phi)_1 + (F_\phi r d \theta dr)_6 - (F_\phi r d \theta dr)_5 \\ &+ (F_\theta r sin \theta dr d \phi )_4 -(F_\theta r sin \theta dr d \phi )_3 \\ & \simeq \frac{\partial (r^2 F_r)}{\partial r} sin \theta dr d \theta d \phi + \frac{\partial F_\phi}{\partial \phi}r dr d \theta d \phi + \frac{\partial (F_\theta sin \theta}{\partial \theta} r dr d \theta d \phi \end{aligned} \end{equation}\]
The volume of the cuboid is
\[dV = r^2 sin \theta dr d \theta d \phi\]
The divergence is then
\[\begin{equation} \begin{aligned} \mathbf{\nabla} \cdot \mathbf{F} &= \frac{\int_S \mathbf{F} \cdot d \mathbf{S}}{dV} \\ &= \frac{\frac{\partial (r^2 F_r)}{\partial r} sin \theta dr d \theta d \phi + \frac{\partial F_\phi}{\partial \phi}r dr d \theta d \phi + \frac{\partial (F_\theta sin \theta}{\partial \theta} r dr d \theta d \phi}{r^2 sin \theta dr d \theta d \phi} \\ &= \frac{1}{r^2} \frac{\partial (r^2 F_r)}{\partial r} + \frac{1}{r sin \theta} \frac{\partial F_\phi}{\partial \phi} + \frac{1}{r sin \theta} \frac{sin \theta F_\theta}{\partial \theta} \end{aligned} \end{equation}\]
