Call Us 07766496223

Similar Articles

facebooktwitter





Log In or Register to Comment Without Captcha

Latest Blog Posts

Derivation of Formula for the Curl of a Vector Dield in Spherical Polar Coordinates

From the cuboid in spherical polar coordinates we can take three faces corresponding to movement in the three coordinate planes.

The first, in the  
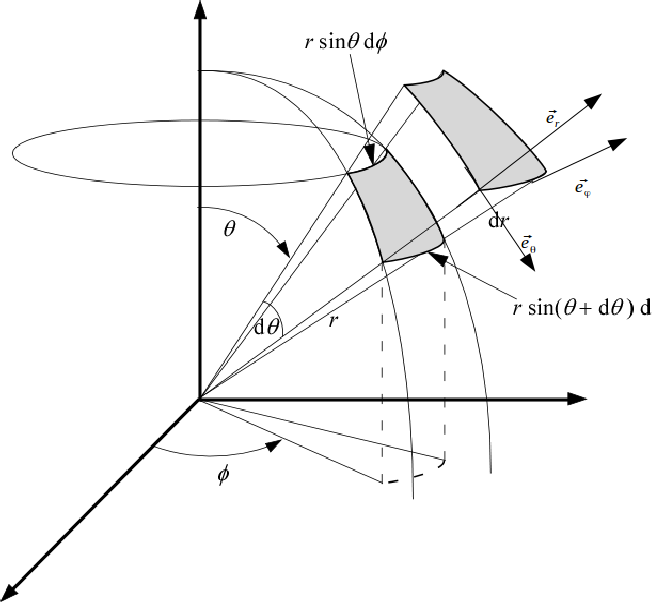
\[\theta - \phi\]
  plane is shown below.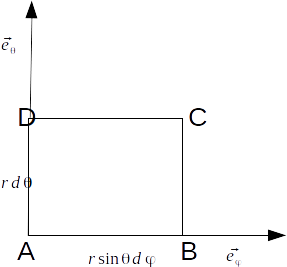

Taking the line integral about ABCD gives
\[(F_\theta r d \theta )_{AB} -(F_\theta r d \theta )_{CD} + (F_\phi r sin \theta d \phi)_{BC} -(F_\phi r sin \theta d \phi)_{DA} \simeq -\frac{\partial F_\theta}{\partial \phi}r d \theta d \phi + \frac{\partial (F_\phi sin \theta )}{\partial \theta}r d \theta d \phi\]

\[curl \mathbf{F} \cdot \mathbf{e_r}= lim_{dV \rightarrow 0} \frac{\oint_{ABCD} \mathbf{F} \cdot d \mathbf{r}}{dV} = \frac{-\frac{\partial F_\theta}{\partial \phi}r d \theta d \phi + \frac{\partial (F_\phi sin \theta )}{\partial \theta}r d \theta d \phi}{r^2 sin \theta dr d \theta d \phi}= \frac{1}{r sin \theta} ( \frac{\partial (F_\phi sin \theta)}{\partial \theta} - \frac{F_\theta}{\partial \phi})\]

The second, in the  
\[r - \theta\]
  plane is shown below.

Taking the line integral about EFGH gives
\[(F_r r dr )_{EF} -(F_r r dr )_{GH} + (F_\theta r d \theta )_{FG} -(F_\theta r d \theta)_{HE} \simeq -\frac{\partial F_r}{\partial \theta}r dr d \theta + \frac{\partial (rF_\theta )}{\partial r}r dr d \theta\]

\[curl \mathbf{F} \cdot \mathbf{e_\phi}= lim_{dV \rightarrow 0} \frac{\oint_{EFGH} \mathbf{F} \cdot d \mathbf{r}}{dV} = \frac{ -\frac{\partial F_r}{\partial \theta}r dr d \theta + \frac{\partial (rF_\theta )}{\partial r}r dr d \theta}{r^2 sin \theta dr d \theta d \phi}= \frac{1}{r} ( \frac{\partial (rF_\theta)}{\partial r} - \frac{F_r}{\partial \theta})\]

The third, in the  
\[r - \phi\]
  plane is shown below.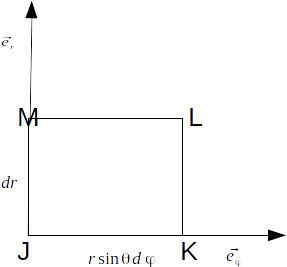

Taking the line integral about JKLM gives
\[(F_\phi sin \theta d \phi )_{JK} -(F_\phi sin \theta d \phi )_{LM} + (F_r dr)_{KL} -(F_r dr)_{MJ} \simeq -\frac{\partial rF_\phi}{\partial r}sin \theta dr d \phi + \frac{\partial (F_r )}{\partial \phi} dr d \phi\]

\[curl \mathbf{F} \cdot \mathbf{e_\theta}= lim_{dV \rightarrow 0} \frac{\oint_{JKLM} \mathbf{F} \cdot d \mathbf{r}}{dV} = \frac{-\frac{\partial rF_\phi}{\partial r}sin \theta dr d \phi + \frac{\partial (F_r )}{\partial \phi} dr d \phi}{r^2 sin \theta dr d \theta d \phi}= \frac{1}{r sin \theta} ( \frac{\partial (F_r)}{\partial \phi} - \frac{rF_\phi}{\partial r} sin \theta)\]

Then  
\[curl \mathbf{F} =\frac{1}{r sin \theta} ( \frac{\partial (F_\phi sin \theta)}{\partial \theta} - \frac{F_\theta}{\partial \phi}) \mathbf{e_r} +\frac{1}{r} ( \frac{\partial (rF_\theta)}{\partial r} - \frac{F_r}{\partial \theta}) \mathbf{e_\phi} + \frac{1}{r} ( \frac{\partial (rF_\theta)}{\partial r} - \frac{F_r}{\partial \theta}) \mathbf{e_\theta} \]