The wave equation is a second order differential equation, and this implies that the the wave function and its first derivative are both continuous across a boundary.
If we assume the wavefunction is described by
then in region I below the wave is described by
since the wave undergoes partial reflection at the boundary at
and in region II it is described by
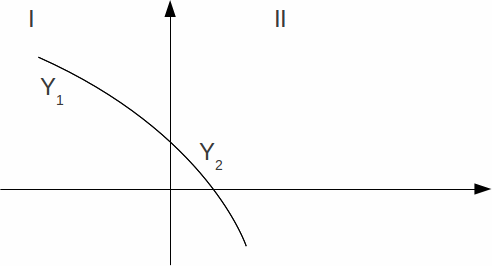
At
and
The first of these implies that
atwhich implies that
hence
(1)
The second implies
(2)
gives
so the transmission coefficient is
gives
so the reflection coefficient is