\[v_1\]
and the speed in medium 2 is \[v_2\]
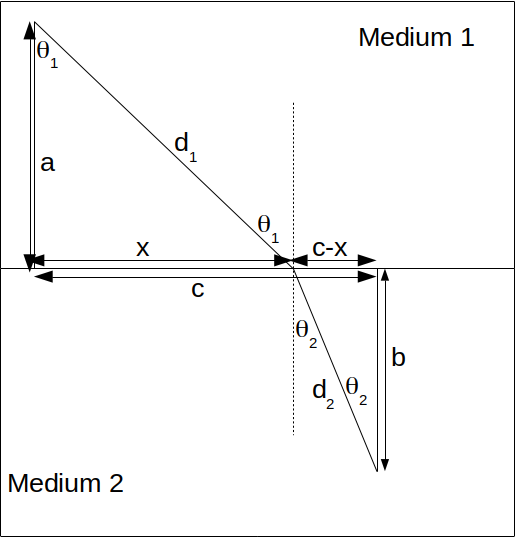
then the time taken to pass from point A to B above is \[t= \frac{d_1}{v_1}+ \frac{d_2}{v_2}= \frac{\sqrt{a^2+x^2}}{v_1} + \frac{\sqrt{b^2+(c-x)^2}}{v_2} = \frac{sin \theta_1}{v_1} + \frac{sin \theta_2}{v_2}\]
.The time is minimised when
\[\frac{dt}{dx} = 0\]
.\[\frac{dt}{dx}= \frac{x}{v_1 \sqrt{a^2+x^2}} - \frac{c-x}{v_2 \sqrt{b^2 + (c-x)^2}}= \frac{sin \theta_1}{v_1}- \frac{sin \theta_2}{v_2}=0\]
.Hence
\[\frac{sin \theta_1}{v_1}= \frac{sin \theta_2}{v_2}\]
.This is one version of Snell's law. Becuase the number of waves passing each point per second - the frequency
\[f\]
- cannot change, and because \[v= f \lambda\]
, where \[\lambda\]
is the wavelength, the frequency is proportional to the wavelength so we can write Snell's Law as \[\frac{sin \theta_1}{\lambda_1}= \frac{sin \theta_2}{\lambda_2}\]
.