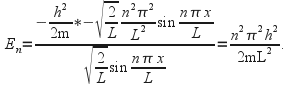The infinite square well potential is given by:
![]()
This is illustrated below.
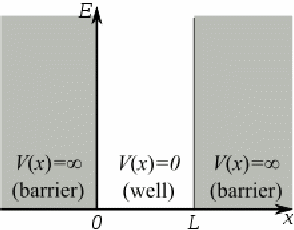
A particle under the influence of such a potential is free - no forces act - between![]() and
and![]() and is confined to that region by the need to have an infinite energy in order to travel outside that region. We can solve the equations describing the motion of the particle in each region and make them fit together at the boundaries using the conditions, for wavefunctions
and is confined to that region by the need to have an infinite energy in order to travel outside that region. We can solve the equations describing the motion of the particle in each region and make them fit together at the boundaries using the conditions, for wavefunctions![]() and
and ![]() on either side of the barriers that
on either side of the barriers that![]() and
and![]()
In the region of the well,![]() and the Schrodinger equation becomes
and the Schrodinger equation becomes![]() (1)
(1)
This has general solution![]() at
at![]() and
and![]() since the potential is infinite there, so
since the potential is infinite there, so![]() so
so![]() and
and![]()
![]()
We can find the constant![]() by requiring that the wavefunction
by requiring that the wavefunction![]() be normalized so
be normalized so![]() We can differentiate
We can differentiate![]() twice to get
twice to get![]() so from (1)
so from (1)