The Schrodinger Equation

The general equation expressing the conservation of energy of a particle in classical mechanics isIn quantum mechanics we have something very similar, with the intoduction of a concept called the wavefunction.

or equivalently

The first of these is called the time independent Schrodinger equation. Time does not appear anywhere in the equation. E on the right hand side is the energy and this equation fully expresses the principle of conservation of energy

The time independent Schrodinger equation allows for the evolution of the wavefunction in time. In general the wavefunction may consist of two parts – the space part and the time part. The space partis a function of position only and the time part is a function of time only,

The Schrodinger equation has several important properties.

1. It is linear. This means that if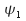and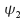are solutions then so is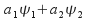and by extension, any linear combination of solutions is also a solution.

2. The equation is second order. This means that given a potential function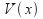in a region, we can solve the equation to find the general solution, but this solution generally contains two arbitrary constants A and B. To find these two arbitrary constants, we need exactly two initial conditions or more typically, boundary conditions or physical constraints to find the constants A and B. The physical constrain may be that the solution must tend to zero as 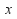tends to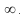

3. Because the Schrodinger equation is second order any solution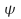or first differential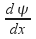must be continuous across a physical boundary. Essentially this mean we can join up the wavefunction on either end of a boundary so that at the boundary both the wavefunction and it's first derivative have the same value.