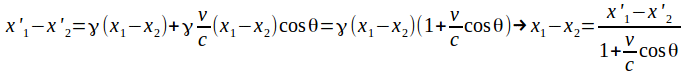Consider a rod at rest in an inertial frame O', with O' moving at speed
along the x axis of an inertial frame O. If the length of the rod in O' is
then in the inertial frame O, an observer will measure the length of the rod to be
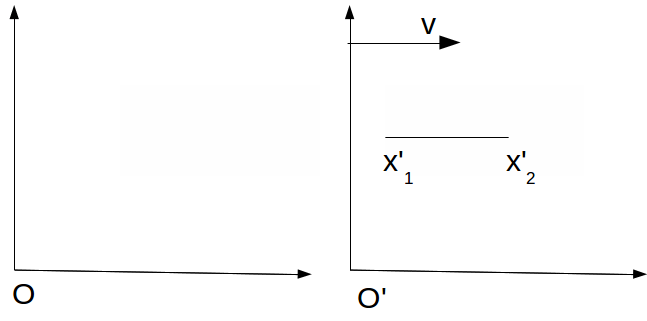
This is not the same as the length of the rod perceived by an observer in O.
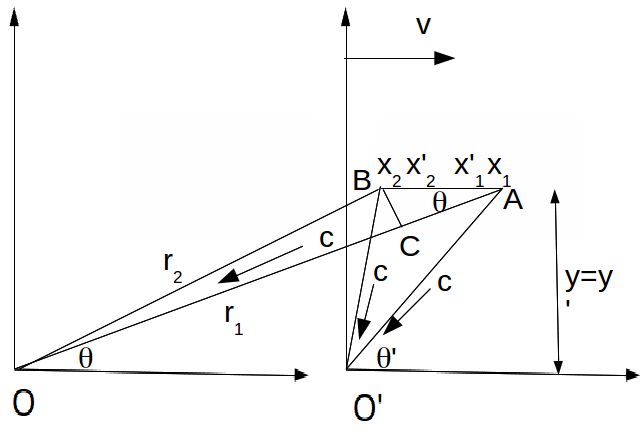
A camera at rest at the origin of O takes a photograph of the rod at
when the origins of O and O' coincide.
The light from the end A of the rod takes a time
to reach O so the light from A was actually emitted at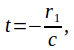
since it reaches the origin of O at
Applying the Lorentz transformation to the emission of the light pulse at A gives
Similarly the light from end B of the moving rod is emitted at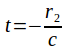
so
Subtracting these gives
From the diagram above
so