\[\kappa\]
with a temperature distribution \[T(x,y,z)\]
the rate of heat flow through a surface drawn in the material is \[H = \int_S - \(\mathbf{\nabla} T) \cdot \mathbf{n} dS\]
Suppose that
\[T=z^2 +6x\]
then \[\mathbf{\nabla} T = 6 \mathbf{i} - 2z \mathbf{k}\]
Take the surface
\[S\]
to be the cuboid shown below.
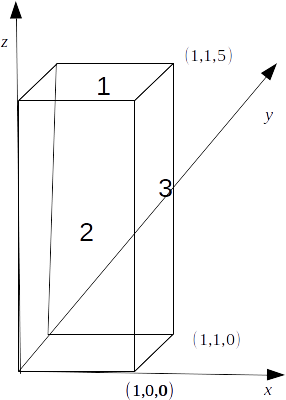
\[\mathbf{j}\]
and \[- \mathbf{j}\]
respectively.\[(\mathbf{\nabla} T) \cdot \mathbf{n} =(6 \mathbf{i} - 2z \mathbf{k}) \cdot pm \mathbf{j} =0\]
From surface 2 =, the top and the bottom surface, the normals are
\[pm \mathbf{k}\]
respevtively\[(\mathbf{\nabla} T) \cdot \mathbf{n} =(6 \mathbf{i} - 2z \mathbf{k}) \cdot pm \mathbf{k} =-2z\]
On the bottom surface
\[z=0\]
so only the top surface contributes to the integral.On the leftmost and rightmost surface 3, the normals are
\[+- \mathbf{i}\]
\[(\mathbf{\nabla} T) \cdot \mathbf{n} =(6 \mathbf{i} - 2z \mathbf{k}) \cdot pm \mathbf{i} =6\]
Then
\[\begin{equation} \begin{aligned} H &=\kappa \int_S - (\mathbf{\nabla} T) \cdot \mathbf{n} dS \\ &=\kappa \int_{S_{TOP}} - (\mathbf{\nabla} T) \cdot \mathbf{n} dS_{TOP}+ \int_{S_{FRONT}} - (\mathbf{\nabla} T) \cdot \mathbf{n} dS_{FRONT} + \kappa \int_{S_{BACK}} - (\mathbf{\nabla} T) \cdot \mathbf{n} dS_{BACK} \\ &= -\kappa \int^1_0 \int^1_0 (6 \mathbf{i} + 2z \mathbf{k}) \cdot \mathbf{k} dx dy -\kappa \int^1_0 \int^5_0 (6 \mathbf{i} + 2z \mathbf{k}) \cdot -\mathbf{-} dx dz -\kappa \int^1_0 \int^5_0 (6 \mathbf{i} + 2z \mathbf{k}) \cdot \mathbf{-} dx dz \\ &= -\kappa \int^1_0 \int^1_0 2z dx dy -\kappa \int^1_0 \int^5_0 -6 dx dz -\kappa \int^1_0 \int^5_0 6 dx dz \\ &- -10\kappa \end{aligned} \end{equation} \]
