Suppose a hollow sphere of inner radius
\[a\]
at temperature \[T_q \]
and outer radius \[b\]
at temperature \[T\]
is amde of material of thermal conductivity \[\kappa\]
.
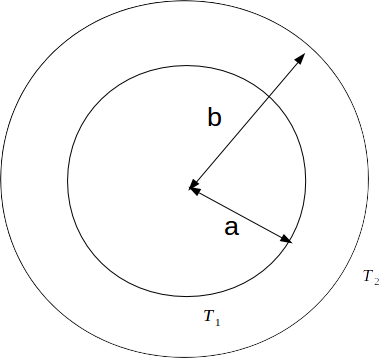
We want to find the temperature as a function of the radius - by symmetry the temperature will depend only on the radius and the normal will be the unit radial vector
\[\mathbf{n} = \mathbf{e_r}\]
. The nrate of heat flow is\[H= \int_s (- \mathbf{\nabla} T) \cdot \mathbf{n} dS= \int_s - \frac{\partial T}{\partial r} \mathbf{e_r}\cdot \mathbf{e_r} dS- =-4 \pi r^2 \kappa \frac{\partial T}{\partial r}\]
When the temperature is steady
\[H\]
will be constant. We can write \[\frac{H}{r^2} dr = -4 \pi \kappa dT \rightarrow \int^r_a \frac{H}{r^2} dr = -4 \pi \kappa \int^T_{T_1} dT \]
Hence
\[-H(\frac{1}{r} - \frac{1}{a}) = -4 \pi \kappa (T-T_1) \rightarrow T= (-H(- \frac{1}{r} + \frac{1}{a}) +T_a \]
When
\[r=b, T=T_2\]
\[H(\frac{1}{b} - \frac{1}{a}) = 4 \pi \kappa (T_2-T_1) \rightarrow H= \frac{ 4 \pi \kappa (T_2-T_1)}{(\frac{1}{b} - \frac{1}{a})}\]
Then
\[-H(\frac{1}{r} - \frac{1}{a}) = -4 \pi \kappa (T-T_1) \rightarrow T= (\frac{ (T_2-T_1)}{(\frac{1}{a} \frac{1}{r})}( \frac{1}{a} - \frac{1}{b}) +T_a \]
