The differential equations![]() is separable We can write this equation as
is separable We can write this equation as![]() Integrating both sides gives
Integrating both sides gives
![]() where
where![]()
Some first order differential equations are not separable. Often the most suitable way to solve it is the integrating factor method, which can be used to solve equations of the form![]()
If we multiply both sides by the integrating factor,![]() the equation becomes
the equation becomes![]() we can write this as
we can write this as![]()
Integrating gives![]() and dividing by
and dividing by![]() gives
gives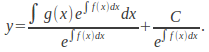 The constant
The constant![]() can be found to solve the initial differential equation if we have simultaneous values of
can be found to solve the initial differential equation if we have simultaneous values of![]() and
and![]() (if we don't have these then we just incliude the integrating constant C – this is the feneral solution).
(if we don't have these then we just incliude the integrating constant C – this is the feneral solution).
Example: Solve the differential equation![]() if
if![]()
![]() so
so![]()
Multiply by the integrating factor to give![]() which we can write as
which we can write as![]() We can integrate this. Obtaining
We can integrate this. Obtaining![]() then dividing by
then dividing by![]() gives
gives![]()
![]() when
when![]() so
so![]() then the solution is
then the solution is![]()
