The moment of Inertia of a body about a point, labelled![]() is found by summing or integrating the moments of inertia of the particles that constitute the body:
is found by summing or integrating the moments of inertia of the particles that constitute the body:
![]() for a collection of discrete particles with masses
for a collection of discrete particles with masses![]() at positions
at positions![]()
![]() where
where![]() with
with![]() equal to the mass of the small region
equal to the mass of the small region![]() of density
of density![]() where
where![]() is the mass of the body at the point and the integral is carried out over the space
is the mass of the body at the point and the integral is carried out over the space![]() (which may be a line, area or volume) occupied by the body
(which may be a line, area or volume) occupied by the body
For example, the moment of inertia of a circular piece of card of uniform mass per unit area![]() and radius
and radius![]() about an axis perpendicular to the card passing through the centre can be found by integration.
about an axis perpendicular to the card passing through the centre can be found by integration.
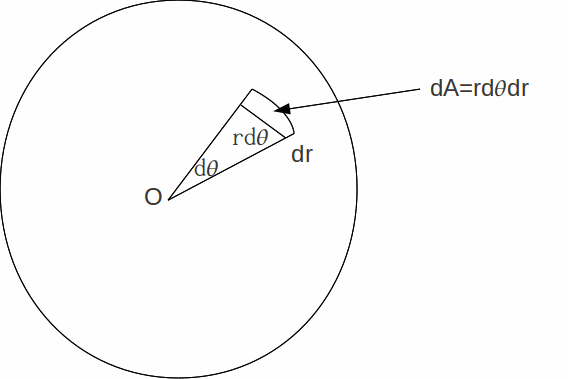
From the diagram above,![]() so
so![]() hence
hence
![]()
The mass of the card is![]() so
so![]()
