\[5 \mathbf{i} + 12 \mathbf{j}\]
with a speed of 12 km/h on a bearing of 70 degrees. Another boat starts from the origin with a speed of 15 km/h to intercept the first ship. How long will it be before interception takes place, and where will interception take place?The diagram illustrates the problem.
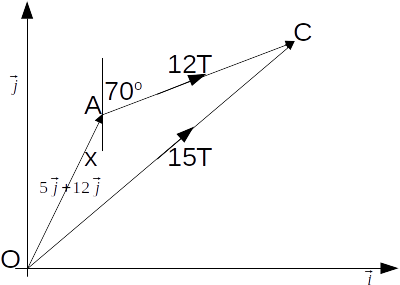
\[(180-70)+tan^{-1}(\frac{5}{12})=132.6^o\]
to 1 decimal place.The distance of A from the origin is
\[\sqrt{5^2+12^2}=13\]
km.The Cosine Rule gives
\[(15T)^2=13^2+(12T)^2-2(13)(12T)cos(132.6)\]
\[225T^2=169+144T^2+211.2T\]
\[81T^2-211.2T-169=0\]
\[T=\frac{211.2 \pm \sqrt{(-211.2)^2-4(81)(-169)}}{2 \times 81} = -0.64, \; 3.25 \]
hours.Obviously the solution is 3.25 hours hours, and interception takes place 15(3.25)=48.75 km from the origin.
