The angular momentum of a rigid body is labelled![]() or
or![]() and is for a rigid body equal in magnitude to the moment of inertia of a body about the axis of rotation times the angular velocity:
and is for a rigid body equal in magnitude to the moment of inertia of a body about the axis of rotation times the angular velocity:![]()
Angular momentum is important because in the absence of any net external torque about the axis of rotation, it is a conserved quantity.
If an external torque![]() is applied to a body of moment of inertia
is applied to a body of moment of inertia![]() then the body will accelerate. The angular velocity
then the body will accelerate. The angular velocity![]() will change. The angular acceleration of the body about the axis of rotation is
will change. The angular acceleration of the body about the axis of rotation is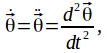 then
then![]()
Integrating this expression with respect to time gives![]()
If not external torques are applied, so that![]() then
then![]()
If the body is not rigid, then the moment of inertia of the body is not constant. Angular momentum is still conserved in the absence of external torques, but![]() becomes
becomes![]()
