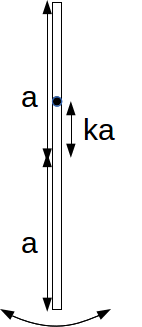
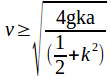If a thin rod of length a is pivoted about a point not at the centre of the rod so that it is able to move in a vertical plane, it will execute circles in a vertical plane if it is given an impulse big enough.
Suppose a rod of length
is pivoted about a point
from the centre, where
The moment of inertia of the rod about the centre is
and the parallel axis theorem gives the moment of inertia of the rod about the pivot point as
where
is the distance of the pivot from the centre of gravity. Hence
If the rod is given a horizontal impulse at the bottom, the kinetic energy given by the impulse must be at least equal to the gravitational potential energy gained by the rod when it has turned through half a circle.
The kinetic energy given to the rod is
The gravitational potential energy gained by the rod is
The condition for vertical motion is
Substitute
to give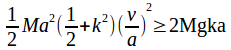
which simplifies to
Then