Proof of Conservation of Angular Moentum

The angular momentum of a rigid body is labelledorand is for a rigid body equal in magnitude to the moment of inertia of a body about the axis of rotation times the angular velocity:

Angular momentum is important because in the absence of any net external torque about the axis of rotation, it is a conserved quantity.

If an external torqueis applied to a body of moment of inertiathen the body will accelerate. The angular velocitywill change. The angular acceleration of the body about the axis of rotation is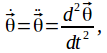then

Integrating this expression with respect to time gives

If not external torques are applied, so thatthen

If the body is not rigid, then the moment of inertia of the body is not constant. Angular momentum is still conserved in the absence of external torques, butbecomes