Solving simultaneous inequalities is not the same as solving simultaneous equations. Simultaneous equations (in
and
) give rise to a set of points. If one equation is linear and the other is quadratic, there are either no points, one point or two points, each of the form
Simultaneous inequalities give rise to ranges ofvalues.
The simplest inequalities are linear. Suppose we have that
and
Showing these inequalities on a number line gives the diagram below. The black circles indicate x may take the values -3, -2 or 1. If
thenmay not take the value -2 and this would be indicated by a hollow circle.
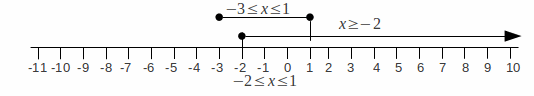
The set ofvalues satisfied by both inequalities is those parts of the– axis 'covered' by both inequalities i.e.
If one inequality is a quadratic our task is slightly harder. Suppose we have
and
Factorising the quadratic gives and equating to 0 gives
so that
or
We can sketch the quadratic to give the graph below.
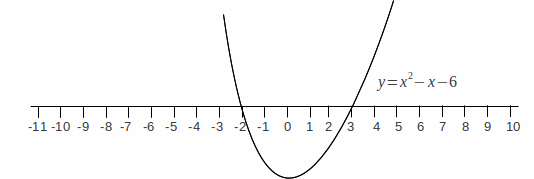
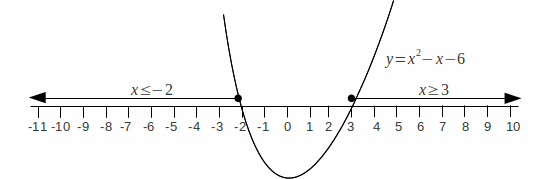
We want those values offor which
– those values offor which the graph is above or on the– axis. These are shown below.
Adding to the diagram the inequality
gives the diagram below.
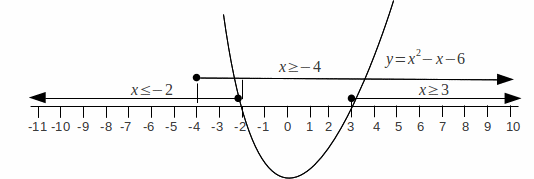
The set ofvalues covered by both is
and