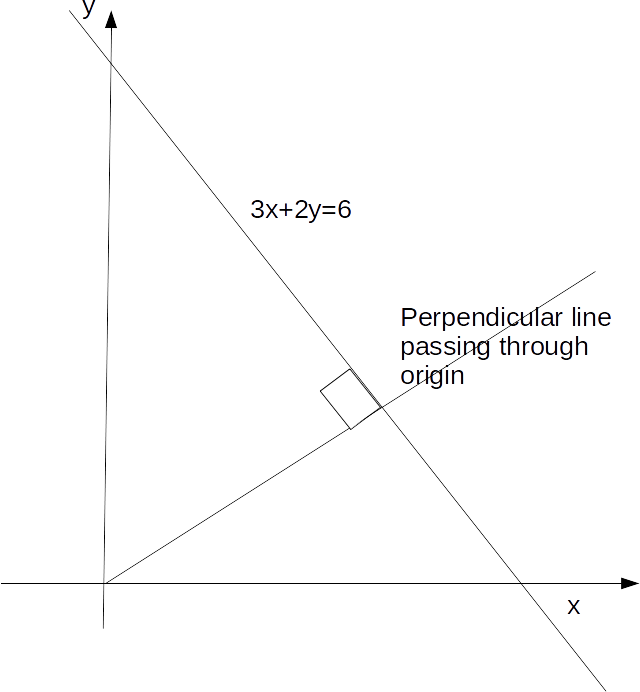
Example: Find the least distance between the line
\[3x+2y=6\]
.
\[y\]
the subject gives \[y=- \frac{3}{2} x +3\]
.This line has gradient
\[- \frac{3}{2}\]
so the perpendicular line has gradient \[- \frac{1}{- (3/2)}=\frac{2}{3}\]
.The equation of the perpendicular line is
\[y= \frac{2}{3}x+c\]
where \[c\]
is the \[y\]
intercept - 0 since the line passes through the origin.The point of intersection of the two lines is the solution to the simultaneous equations
\[y=- \frac{3}{2}x +3\]
\[y= \frac{2}{3}x\]
Subtracting the second from the first gives
\[0=- \frac{13}{6}+3 \rightarrow x=\frac{3}{13/6}=\frac{18}{13}\]
.Then from the second of these equations,
\[y=\frac{2}{3} \times \frac{18}{13}=\frac{12}{13}\]
.
\[d= \sqrt{(18/13)^2+(12/13)^2}=\frac{6 \sqrt{13}}{13}\]
