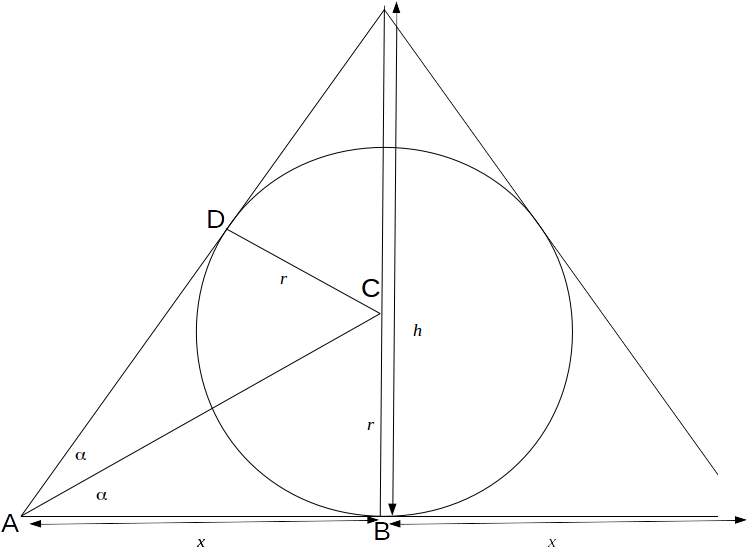
\[\alpha\]
.Then
\[tan \alpha = \frac{r}{x}\]
and \[tan 2 \alpha = \frac{h}{x}\]
Use the identity
\[tan 2 \alpha = \frac{2 tan \alpha}{1- tan^2 \alpha}\]
to obtain \[\frac{h}{x} = \frac{2r/x}{1- r^2/x^2}\]
.This equation can be rearranged to give
\[r^2 h + 2rx^2-hx^=0\]
The solutions to this equation are
\[r=-x \pm \sqrt{x^2+h^2}\]
Obviously only the positive option is possible, so
\[r=-x + \sqrt{x^2+h^2}\]
