\[2b\]
and height \[2h\]
.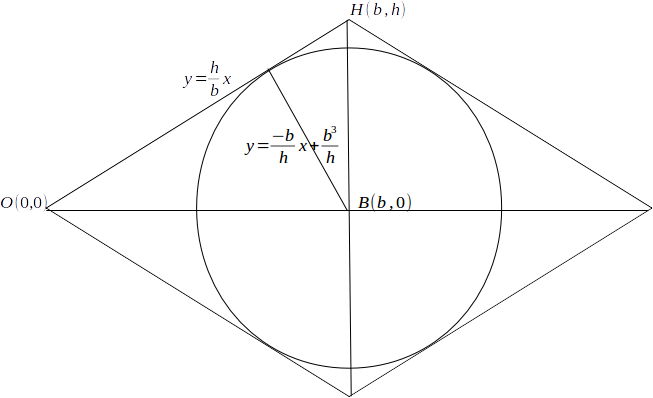
\[y= \frac{h}{b} x\]
.The gradient of the line BH is
\[- \frac{b}{h}\]
and the line passes through the point \[(b,0)\]
.Hence
\[0= - \frac{b}{h} b + c \rightarrow c= \frac{b^2}{h}\]
The equation of the line BH is
\[y= - \frac{b}{h} x + \frac{b^2}{h}\]
Solve simultaneously the equations
\[y = \frac{h}{b} , \: y= - \frac{b}{h} x + \frac{b^2}{h} \]
\[ \frac{h}{b} = - \frac{b}{h} x + \frac{b^2}{h} \rightarrow x(\frac{h}{b} + \frac{b}{h} = \frac{b^2}{h} \rightarrow x= \frac{b^2 /h}{h/b + b /h} =\frac{b^3}{h^2 +b^2}\]
Then
\[y= \frac{h}{b} x = \frac{h}{b} \frac{b^3}{h^2 +b^2}= \frac{b^2 h}{h^2 +b^2}\]
Tthen
\[r = \sqrt{(x-b)^2 + y^2 } = \sqrt{(\frac{b^3}{h^2 +b^2} -b)^2+ (\frac{b^2 h}{h^2 +b^2})^2} =\frac{hb}{h^2+b^2} \sqrt{h^2+b^2} \]
