If two circles intersect and two lines internal two both circles are drawn through the point of intersection, then the chords formed by the points where the lines meet the circles are parallel. In the diagram below, AC is parallel to BD.
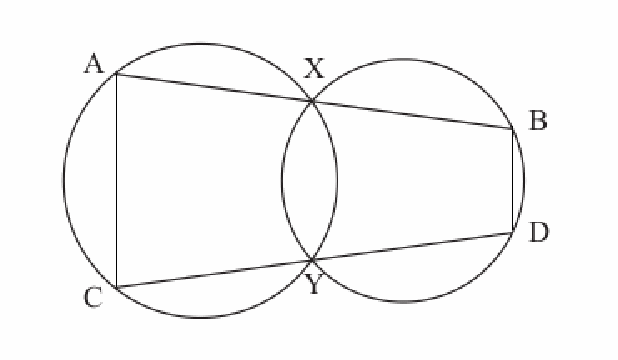
We can prove this using the fact that the quadrilaterals AXYC and BXYD are both cyclic quadrilaterals (the vertices of each quadrilateral lie on a circle).
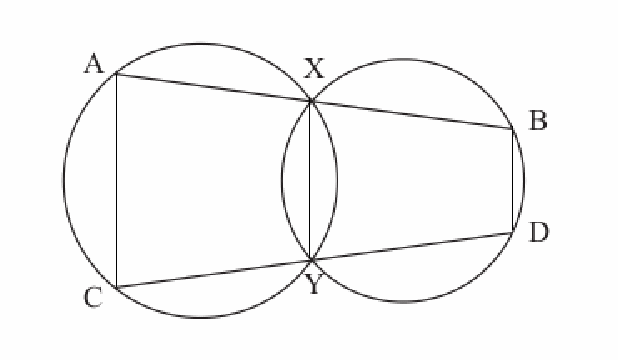
This means that opposite angles CAX and CYX add to 180 degrees and so do YCA and YXA.
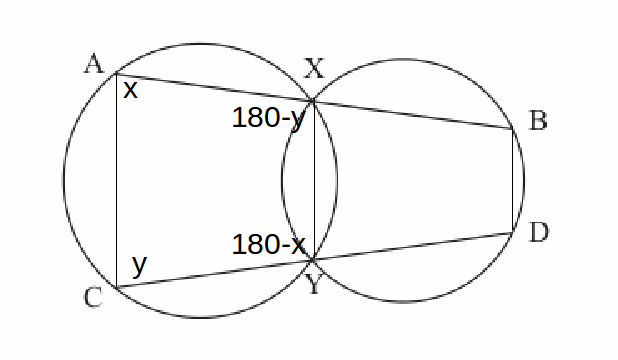
AXB and CYD are straight lines so YXB=180-YXA =180-(180-y)=y
Similarly XYD=x.
Since BXYD is a cyclic quadrilateral, opposite angles add to 180, so YDB=180-y and XBD=x.
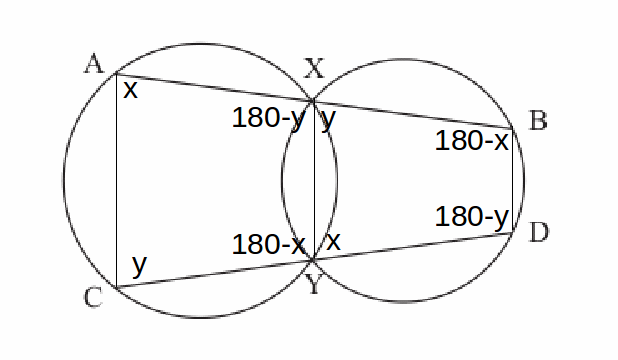
Then CAX and DBX are complementary angles (they add to 180 degrees), and so are angles ACY and BDY. This means that AC and BD are parallel.
