\[sin^2 x cos^2 x =1\]
, draw a right angled triangle, let an angle be \[x\]
and label the sides for that angle.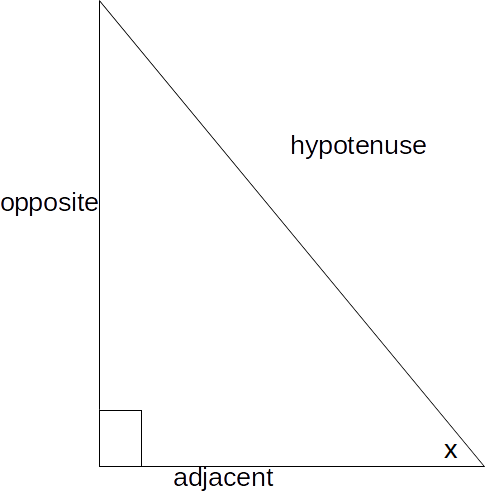
\[opposite^2+adjacent^2=hypotenuse^2\]
Now divide by
\[hypotenuse^2\]
\[\frac{opposite^2}{hypotenuse^2}+\frac{adjacent^2}{hypotenuse^2}=1\]
But
\[\frac{opposite}{hypotenuse}=sin \: x, \frac{adjacent}{hypotenuse}=cos \: x\]
Hence
\[sin^2 x +cos^2 x =1\]
. 