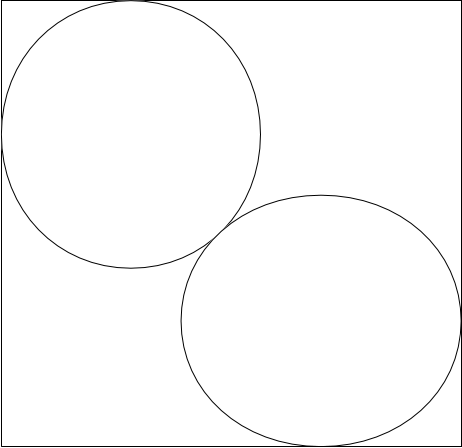
\[x\]
and the radius of the circle is \[r\]
, what is \[r\]
in terms of \[x\]
?We can form small sqaures bewttn the centre of each circle and the nearest vertex of the square.
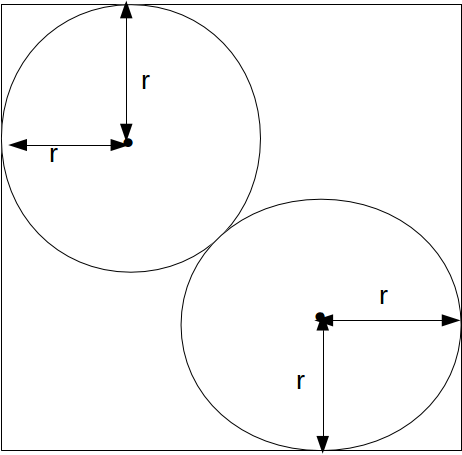
\[\sqrt{r^2+r^2}= r \sqrt{2}\]
.The distance between the centres of the circles is
\[2r\]
.In terms of
\[r\]
, the length of the diagonal of the whole square is \[r \sqrt{2} +2r + r \sqrt{2}=r(2+2 \sqrt{2}) \]
.In terms of
\[x\]
, the length of the diagonal of the whole square is \[\sqrt{x^2+x^2}= x \sqrt{2}\]
.Equating these
\[r(2+2 \sqrt{2})=x \sqrt{2} \rightarrow r =x \frac{\sqrt{2}}{2+2 \sqrt{2}}=x \frac{2- \sqrt{2}}{2}\]
.