Tangents and Normals

A tangent or normal to a curve is a line, taking the formwhereis the gradient andis the intercept. Given a functionwe can find the gradient atby finding the gradient functionand substituting the valueinto this expression. Sometimes however we don't havesois not given explicitly as a function ofIn these cases typically we have to differentiate implicitly and findas a function of bothandand then substitute a pointinto the expression forto find the gradient at that point. Finally substitute into the equationto find the equation of the line.

Example: Find the equation of the tangent to the curveat the point

We differentiate implicitly to getThe gradient at the point is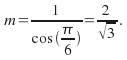

Example: Find the equation of the tangent to the curveat the point

We differentiate implicitly to getWe have to makethe subject of this equation.

The gradient at the point is

Example: Find the equation of the normal to the curveat the point

We differentiate implicitly to getWe have to makethe subject of this equation.

The gradient at the point is