The Order of an Algorithm

Suppose in a room full of people, every person is to shake hands with every other person. If the arepeople, a particular persona shakes hands with all the otherpeople. The shaking of hands is repeated until all thepeople have shaken hands with the otherpeople. It might be thought there arehandshakes altogether. In fact, we have double counted because if person A shakes hands with person B then person B has shaken hands with person A. To avoid this double counting, we must divide by 2, so the number of handshakes is

The highest power ofin this expression is 2, so the order of the handshaking problem is 2. This means that if the number of people doubles fromtothe number of handshakes increases by a factor of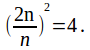

Usually we wish to minimise the number of calculations or steps needed to carry out an algorithm. This means that lower order algorithms are desirable. There are many sorting algorithms. The bubble sort and insertion sort both have order 2, so there areterms in expressions for the number of steps to carry out the algorithm. The quicksort has order less than 2 for many lists (in the worst case scenario it also has order 2). In fact the number of steps for the quicksort typically varies asSinceless steps are required to use the quicksort algorithm for sufficiently high values ofthan wither the bubble sort and insertion sort.