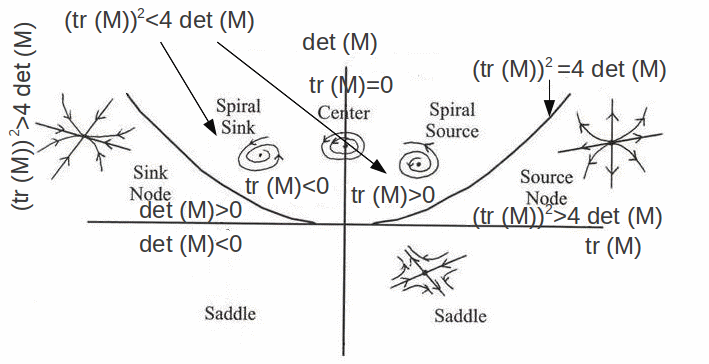
When the velocity representing the motion of a system is linearised about a fixed point, to find the nature of the fixed point, the eigenvalues may be found. For a two dimensional system with a linearisation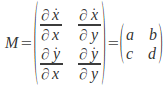
about a fixed point, the eigenvalues are the solution to
This means that the nature of the fixed point is determined completely by the trace and determinant of the linearisation matrix
as long as
This is illustrated below.
