\[\dot{x}=F(x,y)\]
\[\dot{y}=G(x,y)\]
This system may be very difficult or impossible to solve, but we can find the nature of the solution about a point
\[(x_0,y_0)\]
by linearising the system about the point \[(x_0,y_0)\]
\[\dot{x}=\frac{\partial F}{\partial x}|_{(x_0, y_0)}(x-x_0) +\frac{\partial F}{\partial y}|_{(x_0, y_0)}(y-y_0) + higher \: order \: terms\]
\[\dot{y}=\frac{\partial G}{\partial x}|_{(x_0, y_0)}(x-x_0) +\frac{\partial G}{\partial y}|_{(x_0, y_0)}(y-y_0) + higher \: order \: terms\]
We can define
\[x'=x-x_0, \: y'=y-y_0\]
and the system becomes, in matrix form:\[\begin{pmatrix}\dot{x}'\\ \dot{y}'\end{pmatrix} = \left( \begin{array}{cc} \frac{\partial F}{\partial x}|_{(x_0, y_0)} & \frac{\partial F}{\partial y}|_{(x_0, y_0)} \\ \frac{\partial G}{\partial x}|_{(x_0, y_0)} & \frac{\partial G}{\partial y}|_{(x_0, y_0)} \end{array} \right) \begin{pmatrix}x'\\ y'\end{pmatrix} \]
We are especially interested in the point(s)
\[(x_0,y_0)\]
that satisfy \[\dot{x}=\dot{y}=0\]
. These are called critical points.The linearisation matrix
\[\left( \begin{array}{cc} \frac{\partial F}{\partial x}|_{(x_0, y_0)} & \frac{\partial F}{\partial y}|_{(x_0, y_0)} \\ \frac{\partial G}{\partial x}|_{(x_0, y_0)} & \frac{\partial G}{\partial y}|_{(x_0, y_0)} \end{array} \right)\]
has eigenavlues \[\lambda_1 , \: \lambda_2\]
and corresponding eigenvectors \[\mathbf{v}_1, \: \mathbf{v}_2\]
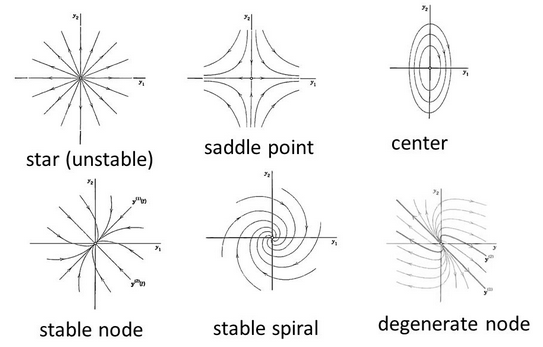
.If
\[\lambda_1 \: \lambda_2 \lt 0\]
then the point \[(x_0, y_0)\]
is stable. Any initial point on the eigenline (a line at starting at the point \[(x_0, y_0)\]
in the direction of an eigenvector) will tend to the point \[(x_0, y_0)\]
along that eigenline. Any initial point not on an eigenline will tend to the eigenline will the eigenline with the corresponding most negative eigenvalue, then towards the point \[(x_0, y_0)\]
. This is a stable node.If
\[\lambda_1 \: \lambda_2 \gt 0\]
then the point \[(x_0, y_0)\]
is unstable. Any initial point on the eigenline will tend to move away from the point \[(x_0, y_0)\]
along that eigenline. Any initial point not on an eigenline will tend to the eigenline will the eigenline with the corresponding most positive eigenvalue, then away from the point \[(x_0, y_0)\]
. This is an unstable node.If
\[\lambda_1 \gt 0, \: \lambda_2 \,t 0\]
then the point \[(x_0, y_0)\]
is unstable. Any initial point not on the eigenline corresponding to \[\lambda_2\]
will tend to the point \[(x_0, y_0)\]
.Any other initial point on the eigenline corresponding to \[\lambda_1\]
will tend to move away from the point \[(x_0, y_0)\]
along that eigenline, or will tend to that eigenline away from the point \[(x_0, y_0)\]
.This is a saddle point.If the eigenvalues are complex
\[\lambda_1=a+bi, \: \lambda_2 =a-bi\]
then if \[a \lt 0\]
the point \[(x_0, y_0)\]
is stable (a stable spiral) and unstable (an unstable spiral)if \[a \gt 0\]
. If \[a = 0\]
then any point will move in a circle about the point \[(x_0, y_0)\]
. The point \[(x_0, y_0)\]
is a centre.If there is only one eigenvalue
\[\lambda\]
and only one eigenvector \[\mathbf{v}\]
then the point \[(x_0,y_0)\]
is a stable degenerate node if \[\lambda \lt 0\]
and an unstable degenerate node if \[\lambda \gt 0\]
.