Bellman's Principle of Optimality is a principle used in directed networks, where arcs can only be traversed in a certain direction.. Suppose we have the network below:
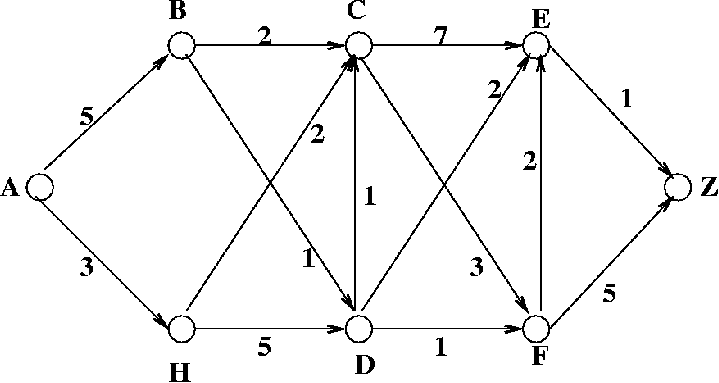
The longest route from A to Z is AHDCEZ. The longest route from A to H is AH. The longest route A to D is AHD. The longest route from A to C is AHDC. The longest route from A to E is AHDCE. The longest route from H to D is HD. The longest route from H to C is HDC. The longest route from H to E is HDCE. The longest route from D to D to C is DC and the longest route from C to E is CE.
Corresponding results can also be given for the shortest route from A to Z.
This example illustrates a general principle – that the any part of a longest (shortest) path from one node to another in a directed network is itself a longest (shortest) path. This is called Bellman's Optimality Principle. It only applies to vertices on the longest (shortest) route and not between any two vertices.
