Given a network, it is desirable to construct a table showing the minimum distance between any two vertices in the network – this includes the case where vertices are not directly connected. We find the least distance even for indirectly connected verticesFor example given the network below,
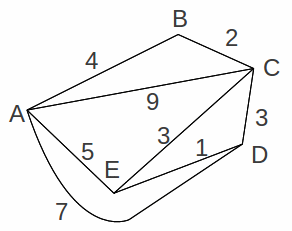
We can go direct from A to C (distance 9), or A to C via B (distance 4+2=6), or from A to C via E (distance 5+3=8), or from A to C via E and D (distance 5+1+3=9), or from A to C via D (distance 7+3=10). The least of all these distance is 6, using the route A to C via B. Gong the the whole network in this way gives us the least distance matrix below.
|
A |
B |
C |
D |
E |
|
|
A |
- |
4 |
6 |
6 |
5 |
|
B |
4 |
- |
2 |
5 |
5 |
|
C |
6 |
2 |
- |
3 |
3 |
|
D |
6 |
5 |
3 |
- |
1 |
|
E |
5 |
5 |
3 |
1 |
- |
Notice that the only blank spaces are between vertices and themselves.
