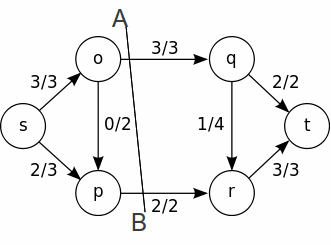
Flows model situations where fluids of some sort – though they may in fact be traffic flows or currents for example - are transported from point to point. The simplest situations involve a single point where fluid flows into the network, called a source, and a single point where fluid exits from the network, called a sink.
The fluid flows along arcs or edges between vertices, with each vertex obeying a simple conservation law, that the total fluid in equals the total fluid out. Each edge or arc has a capacity which represents the maximum possible flow along it, with notation flow/capacity, as illustrated below, though others are possible.
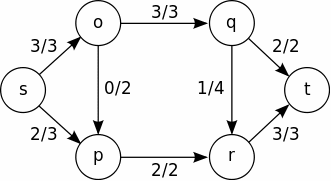
A set of flows though a network is possible – or feasible – if:
-
The total inflow from all source vertices equals the total outflow to all sink vertices.
-
Each vertex obeys a 'conservation of fluid' law, so that for each vertex, toital inflow equals total outflow.
-
The flow along each edge is less than or equal to its capacity.
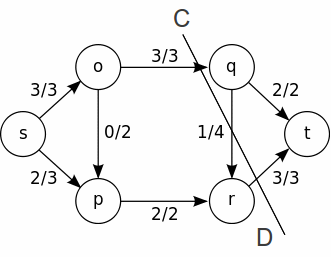
If a flow is feasible we can find the total flow through the network by taking a cut. A cut splits the network into two, one part containing all the sources and the other containing all the sinks, The total flow through the network is then the sum of the flows from the source side to the sink side.