Bernoulli's Equation for a Steadily Flowing Liquid

The Navier - Stokes equation is- a complicated equation which is difficult to solve, except in situation allowing much simplification. If we make the following assumptions, many of important features of the flow are retained.

1. The fluid is inviscid, so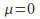and the last term of the Navier – Stokes equation disappears.

2. The fluid is incompressible. This means we can divide each term of the Navier – Stokes equation by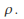The first term on the right becomes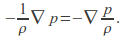

3. The flow is steady, so

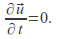
With these assumptions, the Navier – Stokes equation becomes

We now use the identityto obtainIf the force fieldis conservative we can writehence(1).

We can integrate this equation along a streamline. Suppose that s is a parameter for the streamline, thenis a tangent vector to the streamline. Take the dot product ofwith both sides of (1) to give

(2).

is perpendicular to bothandbutis parallel toso When we integrate (2) along a streamline the term on the right hand side returns 0. Since the streamline is arbitrary we havealong a streamline.