The 'travelling salesman problem' is, for a given network of vertices connected by arcs of given lengths, to find the minimum distance that visits each vertex once and returns to the starting vertex.
For a small network, it is possible to find the minimum distance by examining every possible route, but as the size of the network grows, so does the number of routes that must be examined. It is helpful to find upper and lower bounds for the minimum distance.
A lower bound can be found using the following algorithm
-
Choose a vertex and delete it along with all edges connected to it.
-
\Find a minimum spanning tree for the remaining network.
-
Add the length of the minimum spanning tree to the lengths of the two shortest deleted edges.
-
Repeat steps 1 – 3 for each vertex in turn
-
The best lower bound for the path that must be travelled is the largest of the values found.
Given the network below, we apply the algorithm.
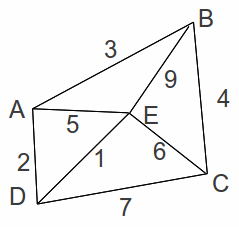
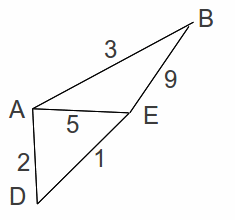
Eliminating A and associated edges gives the network below.
By inspection the minimum spanning tree has length 1+4+6=11. Adding in the two shortest deleted lengths (2 and 3) gives a total length of 16.
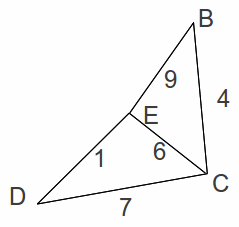
Deleting the vertex B and associated edges gives the network below.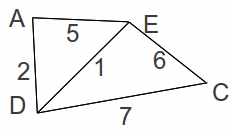
By inspection the minimum spanning tree has length 1+2+6=9. Adding in the two shortest deleted lengths (3 and 4) gives a total length of 16.
Deleting the vertex C and associated edges gives the network below.
By inspection the minimum spanning tree has length 1+2+3=6. Adding in the two shortest deleted lengths (3 and 4) gives a total length of 16.
Deleting the vertex D and associated edges gives the network below.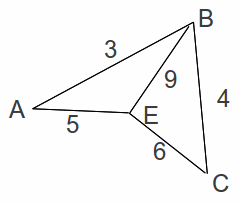
By inspection the minimum spanning tree has length 3+4+5=12. Adding in the two shortest deleted lengths (1 and 2) gives a total length of 15.
Deleting the vertex E and associated edges gives the network below.
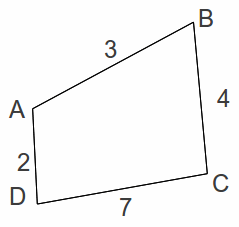
By inspection the minimum spanning tree has length 2+3+4=9. Adding in the two shortest deleted lengths (1 and 5) gives a total length of 15.
The smallest of these values is 15, so the travelling salesman must travel at least 15 length units.
