Advanced Ineqaulities

Inequalities involving modulus functions may be defined analytically over several intervals, and solved in each interval. Your answer may be assisted by a sketch, which will assist you in eliminating unnecessary algebra looking for solutions which do not exist in certain intervals. Sometimes this is the best way to obtain a real picture of what is going on. For example to solve the inequalitywe would sketch the curveand the lineto find where they intersect and then remove the modulus sign – changing the sign if necessary - and solving in that interval.

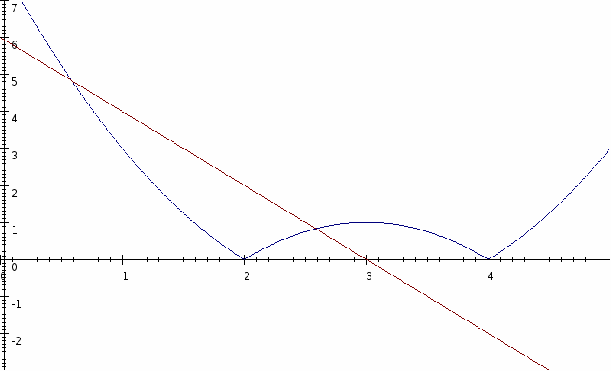
From the graph we can a see solution in the intervalis positive in this region since both factors are negative so multiply to give a positive number.

We solve

By inspection the resulting quadratic equation does not factorise hence we use the quadratic formula

For the quadratic

Onlyis in the intervalso this is the root and because we want the the line to be above the curve we choose and

From the graph we can a see solution in the intervalis negative in this region since one factor is negative and the other positive so multiply to give a negative number. We introduce a minus to allow for this.

We solve

By inspection the resulting quadratic equation does not factorise hence we use the quadratic formula

For the quadratic

From the graph onlyis in the interval sosince we want the line to be above the curve.

Hence