Matrices representing transformations may be multiplied by each other, representing a composition of transformations. We also need to be able to express a matrix as a product of matrices representing transformations. The transformations are are particularly interested in are enlargements or scalings, rotations and reflections.
Suppose then that we have the matrix
This matrix has negative determinant so one of the transformations involved is a rreflection.
The determinant of the matrix is
We can divide each element of the matrix by
to give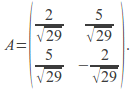
The determinant of this matrix is -1 and the each column and row is of magnitude one so the matrix is a reflection matrix. We can equate this to the reflection matrix and find the angle of rotation.
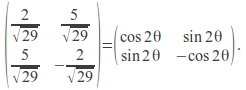
Identifying matrix entries in the upper left and lower left positions gives the equations
Then
The matrix represents an enlargement with scale factor
centre the origin and reflection in the line making an angle of 34.1 degrees with the x axis. The order of transformation in this particular case has no effect because the matrix representing the enlargement is
and this is a multiple of the identity.