Problems of this kind are variable and each one may demand a different approach.
In the diagram below
is the curve
and
is the curve
W e have to find the shaded are and this must be done in several stages.
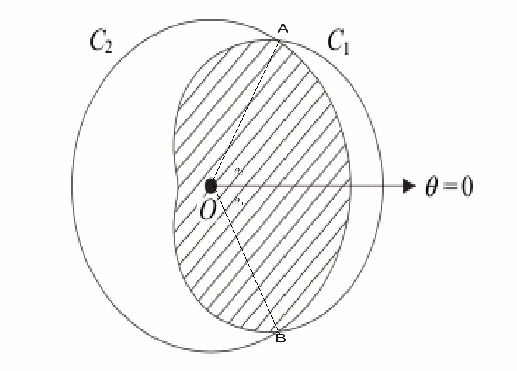
We find the points A and B of intersection of the two curves, specifically, we find the
values 
and
Having found these, the shaded area will consist of the sum of two integrals:
We integrate forthe cardioid between
andand forbetweenand Notice thatis negative.
The pints of intersections are the solutions to
Forwe integrate between
and
or anticlockwise from
The area of the circle between A and B is
The shaded area is the sum of these