Suppose we have a curve which undergoes a linear transformation. The transformation may be represented by a matrix
and the curve by a vector
where
may be a function of
or vice versa, or both are functions of some parameter (I will not deal with this case here).
The simplest case is when a line is transformed. To find the equation of the line
after transformation by the matrix
write line line as the vector
then
Then
and
Makethe subject of both equations and equate the result to give
Now make y' the subject to give
Finally drop the ' to give
More generally we multiply the matrix
by the vectorobtaining
and
in terms ofand
then solve these equations to findandin terms ofand
Finally substitute forandinto the original equation of the curve to obtain an equation relating andFinally drop the ' as in the example above.
Suppose that the curve
is rotated by
The matrix representing this rotation is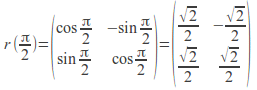
and
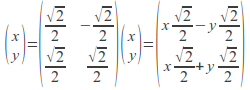
Then
and
Adding these two equations gives
and subtracting them gives
Substituting these into the original equation of the curve
gives
Expanding the brackets gives
which simplifies to